Recently I joined an algorithms Meetup event, which was targeted at people studying for tech interviews. The event was really useful and it was interesting to hear other people’s perspectives, but this is not the main point of this post! This event is how I came across an algorithm I hadn’t heard of before called Huffman encoding. I’ve looked at quite a few coding interview questions but never heard of this algorithm so I started investigating a few days ago…
TLDR; Huffman encoding is a lossless encoding algorithm, meaning you can encode and decode text without losing any information. Personally I think it’s unlikely to come up in any kind of interview you do, although I have seen someone was unfortunate enough to be asked a Huffman question in a Google interview and it’s probably useful knowledge.
Huffman encoding is a prefix algorithm meaning that no encoded value is a prefix of another encoded value. Why is this useful? It means that you can encode your text in variable length values without any delimiters and still be certain about the meaning. For example, let’s say we encode our text as a=0, b=1, c=10. Now when the value 10 is being decoded, we’re not sure how to decode this, it could be ba or it could be c, on the other hand if we encode our text as a=10, b=11, c=0 then we have no doubt that 1110 should be decoded as ba.
Variations of this are used in compression algorithms and image codecs according to Wikipedia.
In this post I’ll explain the idea of the Huffman algorithm by walking through an example and share my implementation. I found it helpful to explain the ideas in a blog post and I hope someone might find the explanation useful!
Prerequisite Knowledge
It helps here if you understand a MinHeap and a Binary Tree. For this it’s enough to know that a MinHeap is a structure which returns us the minimum value of the heap.
The Idea
The idea of the algorithm is to create a Huffman tree, which is a binary tree where the leaves correspond to one character to be encoded. We encode the path from root to leaf using the convention that each left move is ‘0’ and each right move ‘1’. This helps us achieve the prefix effect, because it means that no character is an ancestor of any other (because the characters are all leaves). We create other ‘internal nodes’ for the non-leaf nodes. The input to the algorithm is a set of character frequencies.
We use a MinHeap to store the frequencies and the characters to be encoded, and take the smallest frequencies first so that the most frequent characters are encoded nearer the top of the tree.
Example
Let’s go through an example. First let’s look at the input frequencies:
character Frequency
a 5
b 9
c 12
d 13
e 16
f 45
Example source: GeeksforGeeks.
Initialisation
Remember, we are building a tree but we’re going to do this in a way that’s not obvious. To start with each of these characters and its frequency is in a MinHeap. They each will be a node in a tree but we haven’t yet defined the positions in the tree. I’m going to represent them as a Huffman Node (HN) object HN(char, freq, left, right) where the left and right attributes might not be present initially.
We create a MinHeap with these initial characters and frequencies, so we have HN(a, 5), HN(b, 9), HN(c, 12) etc, so there are 7 HN’s in our MinHeap to start with.
Iterations of Building the Tree
In each iteration we pop the two smallest frequencies from the MinHeap, so in our very first iteration that’s HN(a, 5) and HN(b, 9). We combine the sum of the frequencies into a new object, call it n1. Additionally we set the smallest of our two popped nodes as the left and the largest as the right. So we create a new object HN(n1, 14, left=HN(a, 5), right=HN(b, 9)) and push it back to the MinHeap. Maybe you can see the idea for how we are implicitly building the tree.
We repeat this process, in the second iteration combining HN(c, 12) and HN(d, 13) into HN(25, n2, left=HN(c, 12), right=HN(d, 13)). We continue doing this, also combining any of the new ’n’ tuples.
Eventually, there will only be one node left, this will be the root of our tree. So, you can see that in each iteration we are building ‘mini-trees’ of three nodes and the parent node is pushed to the MinHeap so that it will later become a child node elsewhere.
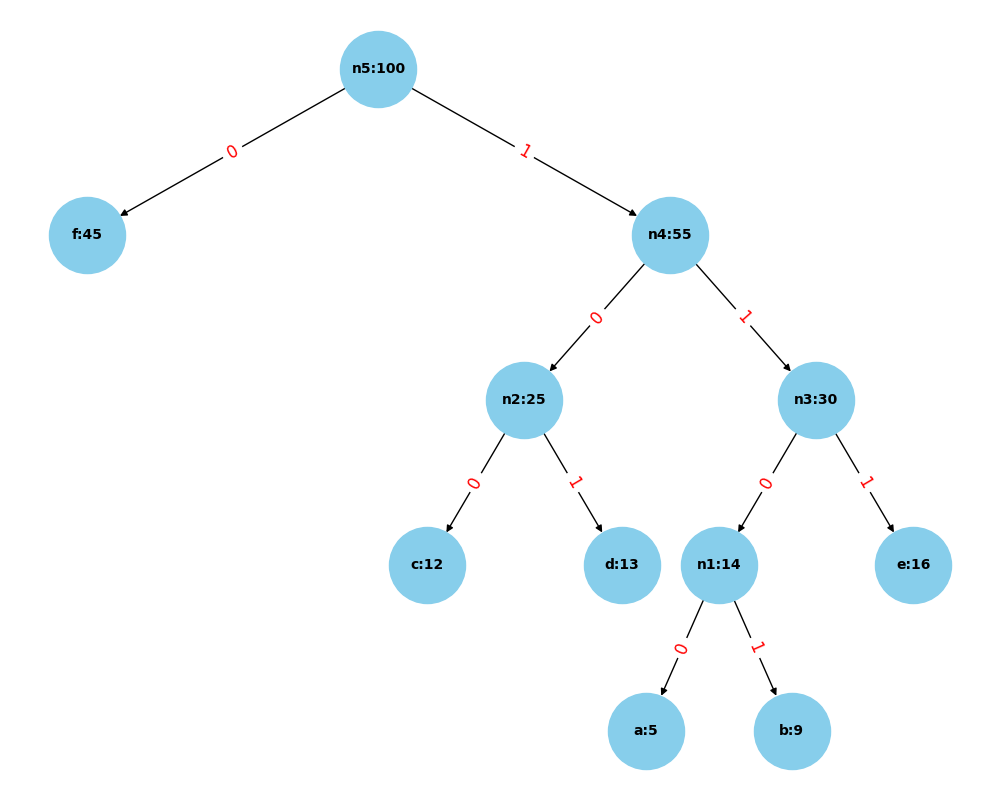
Example Tree
Encoding Characters
So we have built a Huffman tree, but how do we actually encode the nodes? We need to traverse the tree from the root to each node recursively, whilst recording each step of the path as ‘0’ or ‘1’ as mentioned above. For example, in the above tree we go right, left, left to reach the c character, so c will be encoded as 100. It’s helpful to store each of the node’s encodings so that when we iterate through a text it’s fast to retrieve the encoding.
Decoding Encoded Text
Now let’s say we receive some encoded text such as 11001101100, how do we decode this? We iterate through the text, traversing the tree until we reach a leaf. So, for example we start at the root and see 1, so we move right and so on until we see that 1100 corresponds to ‘a’. Now we move to the next character of the encoded text and start again at the root, noticing that 1101 corresponds to ‘b’ and finally 100 means ‘c’, so we have decoded the text as ‘abc’.
Implementation
To implement the algorithm I used two classes, HuffmanEncoder and HuffmanNode. The methods in HuffmanEncoder correspond to the paragraphs above, so the _build_tree method initialises the MinHeap and builds the tree, returning the root. The _encode_tree method adds the encodings to each node as an attribute. The decode method traverses the tree to decode an encoded string.
Further info and Conclusion
You can see the complete code, plus some tests and the code to generate the graph image above in this github repo.
That’s all for now, I hope you got something from this exploration of the Huffman algorithm! Happy coding!